再次思考深度学习框架的自动求导

刚开始读研的时候，对Pytorch以及Tensorflow的反向求导机制非常感兴趣，于是寻找了大量的资料去了解反向求导的机制。2017年华盛顿大学有一门课程非常棒dlsys,第一个实验关于自动求导，第二个实验关于将自动求导的矩阵计算使用GPU来操作。这个课程让我受益匪浅，然后自己写了一个框架thunder,今天看了karpathy的micrograd，觉得非常有意思，于是再次复习一下反向求导的机制。

什么是自动求导

在数学和计算机代数中，自动微分有时称作演算式微分，是一种可以借由计算机程序计算一个函数导数的方法 这个方法广泛应用于各种深度学习框架中，通过自动求导能够得到反向求导的梯度，从而更新权重。

如何进行自动求导

自动求导的例子

如下一个简单的数学公式$x=-4, z=2x+2+x$,那么$\frac{\partial z}{\partial x}=?$,在这里需要求$x$的梯度为多少。

首先画一张图

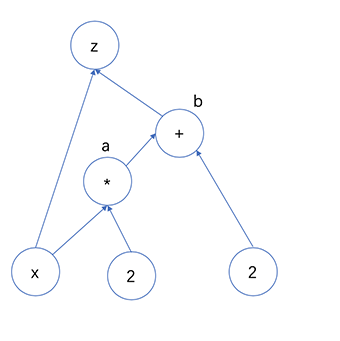
无论是Pytorch或者Tensorflow都是图节点来进行操作。Pytorch是动态图，而Tensorflow静态图（一旦定义就无法修改），从习惯性上来说，Pytorch的动态图更加人性化一点。根据上面的图，可以简单将$\frac{\partial z}{\partial x}$看做是连续求导。如下所示 $$ \frac{\partial z}{\partial x} = \frac{\partial z}{\partial x} + \frac{\partial z}{\partial b} * \frac{\partial b}{\partial a} * \frac{\partial a}{\partial x} = 3 $$ ，其中由于$z$有两个输入，因此需要对$x$进行两次求导，而求导的路径是不同的。经过这个简单的例子，很容易手动算出来，但是如何让计算机进行计算成为重点，因为一旦操作数多，手动算非常耗时且容易出错。

构造自动求导 micrograd

在手动计算中，我们发现了当计算一个节点的时候，我们需要知道它的输入，也就是前驱节点，比如$x$的前驱节点是没有的，因此需要数据结构来保存前驱节点的信息。所以第一步是找出所有的无前驱节点的节点，由于依赖的关系，才能继续求导,那么使用topo排序来得到所有的前驱节点。

1
2
3
4
5
6
7
8

topo = []
visited = set()
def build_topo(v):
    if v not in visited:
        visited.add(v)
        for child in v._prev:
            build_topo(child)
        topo.append(v)

由于topo是从无节点开始push的，因此计算梯度的时候需要反向

1
2

for v in reversed(topo):
    v._backward()

而每一个操作的反向传播是这样的

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

def __mul__(self, other):
    other = other if isinstance(other, Value) else Value(other)
    out = Value(self.data * other.data, (self, other), '*')

    def _backward():
        self.grad += other.data * out.grad
        other.grad += self.data * out.grad

    out._backward = _backward
    return out

对topo中每一个节点进行反向求导，就能够得到每一个变量的梯度。

1
2
3
4
5
6
7
8

def test_sanity_check():
    x = Value(-4.0)
    z = 2 * x + 2 + x

    z.backward()

    assert z.data == -10.0
    assert x.grad == 3.0

参考